Descarga el Taller sobre aplicaciones de los teoremas del Seno y del Coseno.

Taller Número 4 - Teoremas del Seno y el Coseno.doc (29184)

TEOREMAS DEL SENO Y DEL COSENO

Tanto el teorema del seno como el del coseno son resultados que se pueden aplicar a cualquier triángulo, es decir, no nos hace falta que el triángulo sea rectángulo, como nos pasaba con el teorema de Pitágoras.
 
El teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos relativamente opuestos. Dado el triángulo:
     
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Por su parte, el teorema del coseno se puede entender como una generalización del teorema de Pitágoras para triángulos cualesquiera, es decir, si aplicamos el teorema del coseno en un triángulo rectángulo obtenemos el mismo resultado que el teorema de Pitágoras. Nos relaciona la longitud de un lado con las longitudes de los otros y con el coseno del ángulo formado por éstos. Dado el triángulo,
   
 
 
 
 
 
 
 
 
Como puede observarse se tienen 3 igualdades que son basicamente la misma. Se conocen dos lados de un triángulo y el ángulo que forman esos dos lados.
 
 
 

EJEMPLOS DE APLICACIÓN DE LOS TEOREMAS DE SENO Y COSENO

PROBLEMA:

Dos hombres recorren 10 km partiendo desde un mismo cruce y siguiendo dos caminos rectos en el mismo sentido que forman 30º entre ellos. ¿A qué distancia en línea recta se encontraran uno del otro al terminar la caminata?

SOLUCION:

Si dibujamos las trayectorias que siguen ambos hombres obtenemos un triángulo como el de la figura:

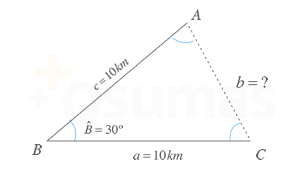
Nuestra misión será calcular su lado b y para ello podemos hacerlo de una manera rápida utilizando el teorema del coseno:

 

RTA: Al terminar la caminata, las dos personas se encontrarán a una distancia aproximada de 5,17 kilómetros.

En la parte inferior encontrarás una selección de ejemplos de aplicación de los teoremas del Seno y del Coseno explicados en video. 

También puedes visitar las siguientes páginas recomendadas para ampliar información y ver más ejemplos.