MÉTODO DE SUSTITUCIÓN
El método de sustitución de un sistema de ecuaciones consiste en sustituir una ecuacioon en otra con el fin de eliminar una de las variables y obtener una ecuación que se pueda resolver. Para ello se realiza el siguiente procedimiento.
- 1. Se despeja una incógnita en una de las ecuaciones.
- 2. Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita.
- 3. Se resuelve la ecuación.
- 4. El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.
- 5. Los dos valores obtenidos constituyen la solución del sistema.
Vamos a resolver por ejemplo el siguiente sistema de ecuaciones:

Para saber en todo momento a qué ecuación del sistema nos referimos, a la ecuación de arriba le llamaremos primera ecuación y a la de abajo segunda ecuación:

1. Despejamos una incógnita en una de las ecuaciones, la más fácil para despejar es la “y” en la primera ecuación, ya que no tiene ningún número delante y además tiene un signo más delante, por lo que tan sólo pasando el 5x al otro lado ya tenemos la y despejada:
![]()
2. En la ecuación que no hemos utilizado, sustituimos la misma incógnita despejada en el paso anterior, por el valor que hemos obtenido. Es decir, en la segunda ecuación, donde aparece y, lo sustituimos por su valor en función de x:
![]()
3. Despejamos la incógnita que nos queda.
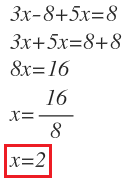
Y obtenemos el valor numérico de x.
4 . El valor numérico obtenido se sustituye en la ecuación donde despejamos una incógnita en función de otra (paso 1). En nuestro caso, donde despejamos y en función de x:
![]()
De donde deducimos que la solucion de este sistema es x=2, y=-2
